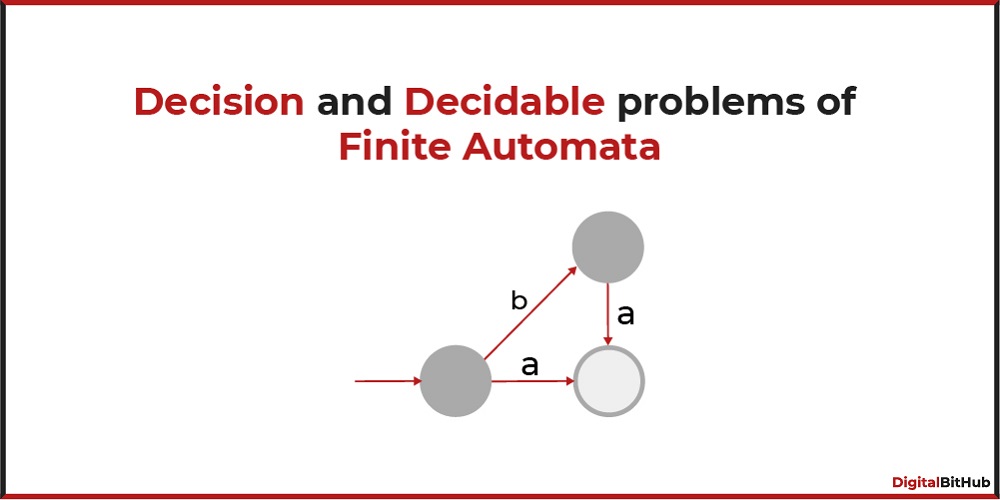
Undecidable problems are computational questions or tasks for which no algorithm can exist to provide a definite answer. These problems have been extensively studied in various branches of computer science and mathematics. Here is a list of some well-known undecidable problems:
Halting Problem
Given a program and an input, determine whether the program will eventually halt or run indefinitely.
Post Correspondence Problem (PCP)
Determine whether a given set of dominos can be arranged to form the same string when their top and bottom strings are concatenated.
Rice's Theorem
Decide any non-trivial property of the behavior of a Turing machine. Examples include determining whether a Turing machine accepts any input, or whether it halts on all inputs.
Entscheidungsproblem
Also known as the Decision Problem, it asks whether there exists an algorithm that can decide the truth or falsity of any given mathematical statement.
Gödel's Incompleteness Theorems
These theorems, proved by Kurt Gödel, state that in any sufficiently powerful formal system, there will always be true statements that cannot be proven within that system.
Tiling Problem
Determine whether a given set of square tiles can completely tile the plane (without overlapping or leaving gaps) when infinite copies are allowed.
Collatz Conjecture
The Collatz Conjecture poses a simple arithmetic sequence where starting from any positive integer, if it is even, divides it by 2; if it is odd, multiply it by 3 and add 1. The conjecture states that no matter the starting number, the sequence will eventually reach 1. However, proving this conjecture for all numbers is an open problem.
Busy Beaver Problem
Find the most productive Turing machine with a given number of states. Productivity is defined as the maximum number of steps the machine halts after starting from a blank tape.
Post's Correspondence Problem for Regular Languages
Determine whether a given set of pairs of strings from regular languages can be arranged to form identical strings when concatenated.
Wang's Domino Problem
Determine whether a given set of square dominos with colored sides can tile the plane to form a chessboard pattern when infinite copies are allowed.
These are just a few examples of undecidable problems that have captured the attention of researchers for many years. The study of undecidability has had a profound impact on computer science, logic, and mathematics, revealing fundamental limitations in the field of computation.