In the vast field of theoretical computer science, one important area of study is the theory of automata. Automata theory deals with mathematical models of computation and their properties. It seeks to understand what can and cannot be computed using various computational models. In this article, we will explore the concepts of decidable and undecidable problems in the theory of automata.
Decidable Problems
Decidable problems refer to those computational questions for which an algorithm can be constructed to determine the correct answer. In simpler terms, given an input, a decidable problem can be solved using a definite, step-by-step procedure. Let's see some examples of decidable problems.
Language Membership
Suppose we have a language L defined as the set of all even-length strings over the alphabet {0, 1}. The problem of determining whether a given string belongs to L is decidable. We can design an algorithm that checks the length of the input string and then verifies if it contains only 0s and 1s. If both conditions are satisfied, we conclude that the string belongs to L.
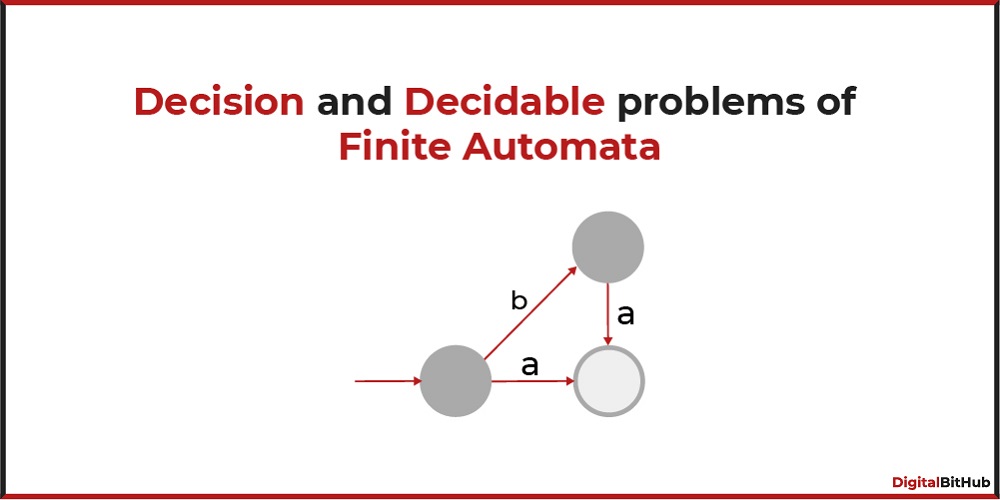
Finite Automaton Acceptance
Consider a finite automaton—a mathematical model used to recognize languages. Given a finite automaton and an input string, the problem of determining whether the automaton accepts the string is decidable. We can construct an algorithm that simulates the automaton's behavior on the input string, following the transition rules, and check if it reaches an accepting state.
Undecidable Problems
In contrast to decidable problems, undecidable problems are those for which no algorithm can be formulated to provide a definite answer. These problems typically involve more complex computations or require examining an infinite number of possibilities. Let's see some examples of undecidable problems.
Halting Problem
The halting problem is a classic undecidable problem in computer science. It asks whether, given a program and an input, the program will eventually halt or run indefinitely. In other words, there is no general algorithm that can determine if a program will halt for all possible inputs.
Post Correspondence Problem (PCP)
The Post Correspondence Problem is another famous undecidable problem. It involves finding a solution to a particular string manipulation puzzle. Given a set of dominos, each with a top and bottom string, the goal is to arrange a sequence of dominos such that concatenating the corresponding top strings produces the same result as concatenating the corresponding bottom strings. Deciding whether a solution exists for a given set of dominos is undecidable.
In summary, decidable problems in the theory of automata can be solved using an algorithm, while undecidable problems do not have an algorithmic solution. Undecidable problems often pose significant challenges in computer science, pushing the boundaries of what can be computed. Although undecidability might appear limiting, it leads to fascinating insights and advancements in theoretical research, helping us understand the fundamental limits of computation.
It's important to note that the examples provided in this article represent only a glimpse of the decidable and undecidable problems in the theory of automata. The field encompasses a wide range of problems and their classifications, contributing to the development of computational models and the exploration of their capabilities.