In the realm of theoretical computer science, two fundamental concepts play a significant role in understanding the capabilities and limitations of computation: decidability and undecidability. These concepts revolve around the ability to determine the answer to a computational problem and have shaped the landscape of theoretical research. In this article, we will delve into the differences between decidability and undecidability, shedding light on their definitions, implications, and impact on the field.
Decidability: The Power of Definite Answers
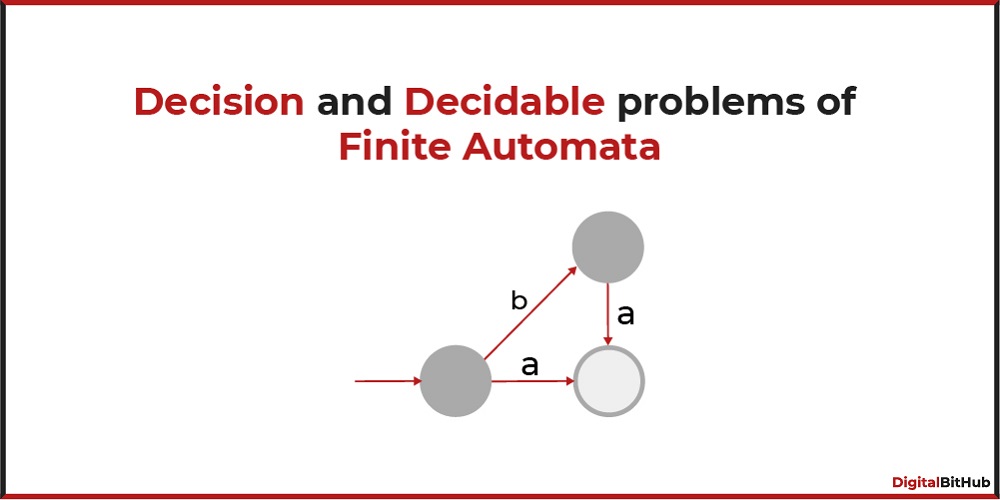
Decidability refers to the property of a problem for which an algorithm exists to provide a definite answer—either "yes" or "no"—for any given instance. Essentially, a decidable problem can be solved using a systematic procedure or algorithm that guarantees a correct and finite answer within a reasonable amount of time. This ability to determine the answer with certainty is a remarkable characteristic of decidable problems.
Undecidability: The Realm of Unanswered Questions
In contrast, undecidability refers to problems for which no algorithm exists to provide a definite answer for all possible instances. In other words, an undecidable problem is one where there is no systematic procedure or algorithm that can determine whether a given instance belongs to the problem's set or not. The existence of undecidable problems signifies the inherent limits of computation.
The concept of undecidability has profound implications in the field of theoretical computer science. It reveals fundamental limitations, highlighting that not all computational questions have definitive answers. The study of undecidable problems drives researchers to explore alternative approaches, heuristics, and restrictions to tackle problems that fall within the realm of undecidability. Undecidability challenges us to think beyond traditional algorithmic solutions and fosters innovation in computational thinking.
Decidability vs. Undecidability: A Comparison
Let's summarize the key differences between decidability and undecidability in a concise manner:
| Decidability | Undecidability | |
| Definition | A problem is decidable if there exists an algorithm that can provide a definite answer for all instances of the problem. | A problem is undecidable if there is no algorithm that can provide a definite answer for all instances of the problem. |
| Answer | Decidable problems have a definite "yes" or "no" answer. | Undecidable problems lack a definite answer for all instances. |
| Algorithms | Decidable problems have algorithms that solve them efficiently. | No algorithm exists to solve undecidable problems for all instances. |
| Examples | Language membership, regular expression equivalence, sorting. | Halting problem, Post Correspondence Problem, Collatz Conjecture. |
| Implication | Decidability implies computability within a finite amount of time. | Undecidability implies inherent limits on what can be computed. |
| Proof | Decidability can often be proven through the existence of an algorithm. | Undecidability is proven through rigorous mathematical proofs. |
| Impact | Decidability allows for efficient problem-solving and algorithm design. | Undecidability poses fundamental challenges and inspires alternative approaches. |
Conclusion
Decidability and undecidability represent two fundamental concepts in theoretical computer science, drawing boundaries around what can and cannot be computed. Decidable problems offer the power of definite answers, enabling efficient algorithmic solutions to computational questions. In contrast, undecidability exposes the existence of problems for which no algorithm can provide definitive answers, challenging our understanding of computation and inspiring innovative thinking.
The study of decidability and undecidability continues to drive advancements in theoretical computer science, shaping the development of algorithms, computational models