What is the Fibonacci series?
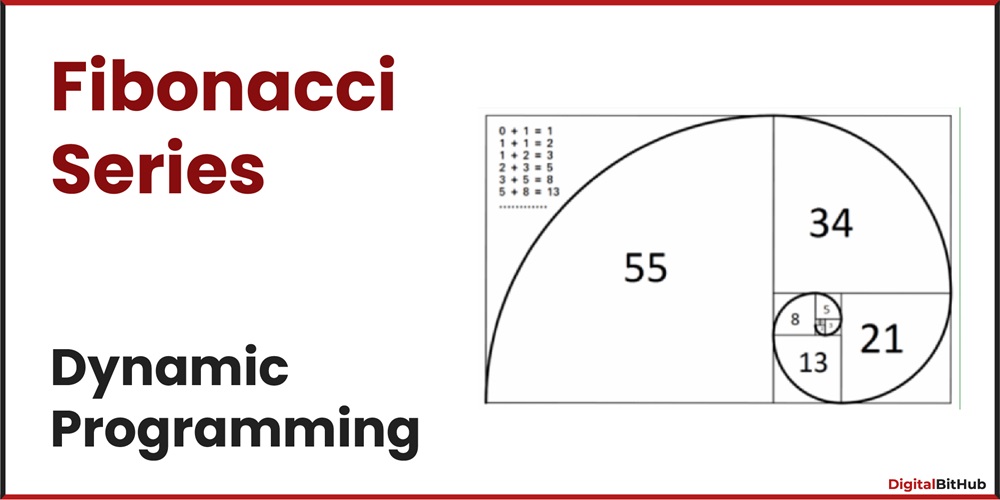
The Fibonacci series is a sequence of numbers in which each number (known as aFibonacci number) is the sum of the two preceding ones, usually starting with 0 and 1. The sequence is
0, 1, 1, 2, 3, 5, 8, 13, 21, 34 .....
Let's start with a problem
Given a number n, find nth Fibonacci Number.
There are various ways to find the nth Fibonacci Number, which includes
- Iterative Approach
- Recursive Approach
- Dynamic Programming Approach
Iterative Approach to Find Fibonacci Number
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation:
Fn = Fn-1 + Fn-2 with initial values F0 = 0 and F1 = 1.
#include <stdio.h>
int fib(int n) {
int a = 0, b = 1, c, i;
if (n == 0)
return a;
for (i = 2; i <= n; i++) {
c = a + b;
a = b;
b = c;
}
return b;
}
int main() {
int n = 7;
printf("%d", fib(n));
getchar();
return 0;
}
The above program will print the 7th Fibonacci number which is 13.
Time Complexity of the above approach is O(n).
Space Complexity is O(1).
Recursive Approach to Find Fibonacci Number
The recurrence relation says that
- F0 = 0, If n == 0
- F1 = 1, if n == 1
- Fn = Fn-1 + Fn-2, if n > 1
// Fibonacci Series using Recursion
#include <stdio.h>
int fib(int n)
{
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}
int main()
{
int n = 7;
printf("%dth Fibonacci Number: %d", n, fib(n));
return 0;
}
The above program will print the 7th Fibonacci number which is 13.
Time Complexity of the above approach is Exponential as every function calls two other functions.
Space Complexity is O(n). The maximum depth of the recursion tree will not exceed n.
Dynamic Approach to Find Fibonacci Number
As we see, in the recursive approach, the time complexity is exponential. Let's take a view of the recursive tree.
fib(5)
/ \
fib(4) fib(3)
/ \ / \
fib(3) fib(2) fib(2) fib(1)
/ \ / \ / \
fib(2) fib(1) fib(1) fib(0) fib(1) fib(0)
/ \
fib(1) fib(0)
When you look closely, you'll notice that the same function calls over and over again with the same input. We can optimize it using Dynamic Programming. Instead of redoing everything each time, we can save the Fibonacci numbers we've already calculated.
Check out the implementation of the dynamic approach.
#include <stdio.h>
int fib(int n)
{
/* Declare an array to store Fibonacci numbers. */
int f[n + 2]; // 1 extra to handle case, n = 0
int i;
/* 0th and 1st number of the series are 0 and 1*/
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++) {
/* Add the previous 2 numbers in the series
and store it */
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
int main()
{
int n = 7;
printf("%d", fib(n));
getchar();
return 0;
}
The above program will print the 7th Fibonacci number which is 13.
Time Complexity is O(n).
Space Complexity is O(n).