Decidable problems are computational questions or tasks for which an algorithm exists to determine the correct answer. These problems have been extensively studied and various algorithms have been developed to solve them efficiently. Here is a list of some well-known decidable problems:
Language Membership
Given a language defined over an alphabet, determine whether a given string belongs to that language.
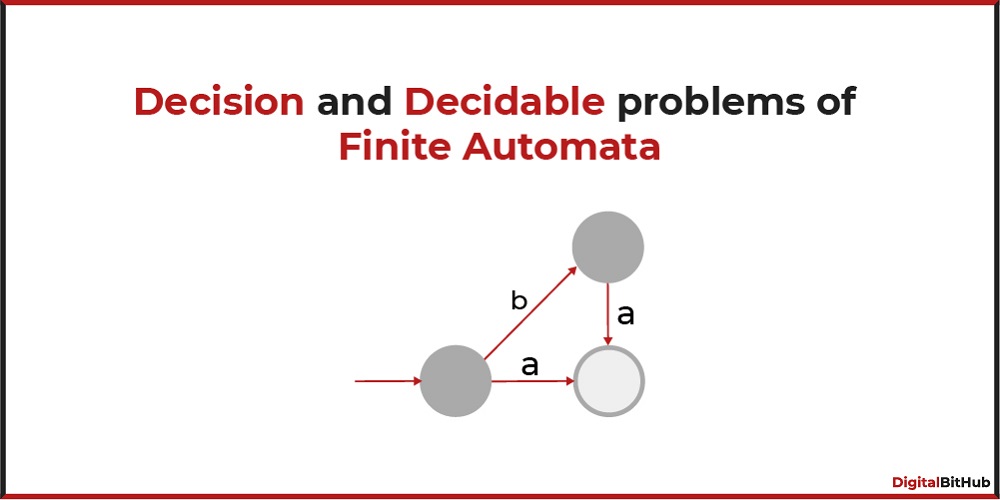
Finite Automaton Acceptance
Given a finite automaton and an input string, determine whether the automaton accepts the string (i.e., reaches an accepting state).
Regular Expression Equivalence
Determine whether two regular expressions describe the same language.
Context-Free Grammar Membership
Given context-free grammar and a string, determine whether the string can be generated by the grammar.
Context-Free Language Emptiness
Determine whether a given context-free language is empty (i.e., it does not contain any strings).
Linear Diophantine Equations
Given a system of linear Diophantine equations, determine whether there exist integer solutions for the variables.
Eulerian Path Existence
Determine whether a given undirected graph has an Eulerian path (a path that visits each edge exactly once).
Primality Testing
Given an integer, determine whether it is a prime number.
Sorting
Given a sequence of elements, determine a sorted version of the sequence in non-decreasing or non-increasing order.
Shortest Path Problem in Directed Acyclic Graphs (DAGs)
Given a directed acyclic graph and two vertices, determine the shortest path between the vertices.
Maximum Flow Problem
Given a flow network and two vertices, determine the maximum amount of flow that can be sent from the source to the sink.
Matrix Multiplication
Given two matrices, compute their product matrix.
Tree Isomorphism
Determine whether two given trees are isomorphic (i.e., they have the same structure).
Linear Programming
Given a system of linear inequalities, determine whether there exists a feasible solution that satisfies all the inequalities.
Two-Satisfiability
Given a Boolean formula in conjunctive normal form (CNF), determine whether there exists an assignment of values to variables that satisfies the formula.
These are just a few examples of decidable problems that have well-established algorithms to solve them efficiently. Decidable problems play a crucial role in algorithm design and are extensively used in various areas of computer science and mathematics.