What is Sorting?
Sorting is a way of arranging items in a specific order, such as numbers from smallest to largest or names alphabetically. This helps computers and people find what they are looking for in a more organized way.
What is a Sorting Algorithm?
A sorting algorithm is a set of instructions or rules that tells a computer how to arrange a list of items in a particular order. Imagine you have an array of numbers, and you want to arrange them in ascending order. A sorting algorithm would be like a set of steps you follow to organize the numbers from the smallest to the largest.
Complexity Comparison of Sorting Algorithms
| Algorithm | Best Case | Average Case | Worst Case | Memory | Stable | Method Used |
|---|---|---|---|---|---|---|
| Quick Sort | nlogn | nlogn | n2 | nlogn | No | Partitioning |
| Merge Sort | nlogn | nlogn | nlogn | n | Yes | Merging |
| Heap Sort | nlogn | nlogn | nlogn | 1 | No | Selection |
| Insertion Sort | n | n2 | n2 | 1 | Yes | Insertion |
| Tim Sort | n | nlogn | nlogn | n | Yes | Insertion & Merging |
| Selection Sort | n2 | n2 | n2 | 1 | No | Selection |
| Shell Sort | nlogn | n4/3 | n3/2 | 1 | No | Insertion |
| Bubble Sort | n | n2 | n2 | 1 | Yes | Exchanging |
| Tree Sort | nlogn | nlogn | nlogn | n | Yes | Insertion |
| Cycle Sort | n2 | n2 | n2 | 1 | No | Selection |
| Strand Sort | n | n2 | n2 | n | Yes | Selection |
| Cocktail Shaker Sort | n | n2 | n2 | 1 | Yes | Exchanging |
| Comb Sort | nlogn | n2 | n2 | 1 | No | Exchanging |
| Gnome Sort | n | n2 | n2 | 1 | Yes | Exchanging |
| Odd Even Sort | n | n2 | n2 | 1 | Yes | Exchanging |
There are various types of sorting algorithms in computer science.
- Selection Sort
- Bubble Sort
- Insertion Sort
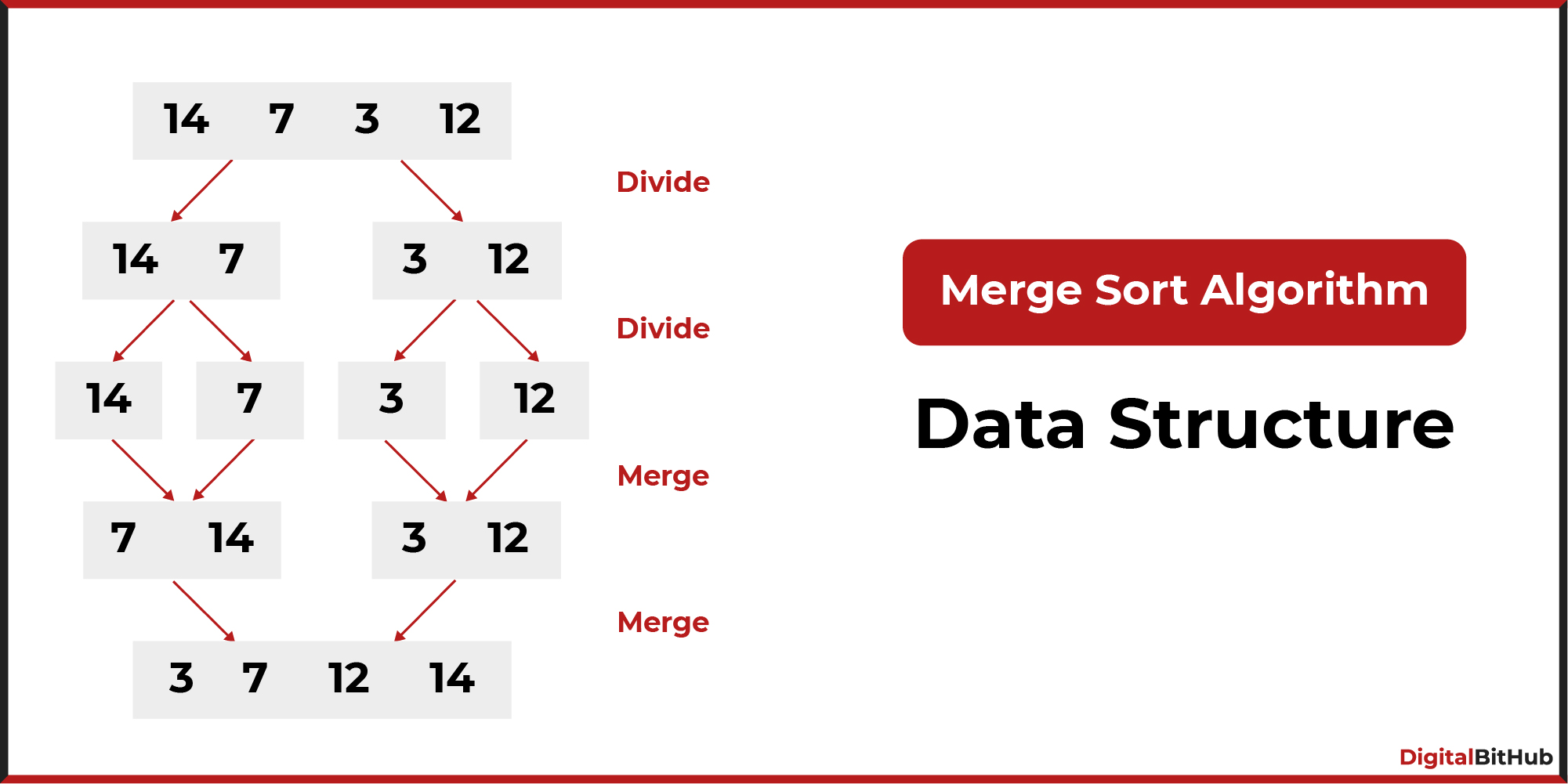
- Merge Sort
- Quick Sort
- Heap Sort
- Counting Sort
- Radix Sort
- Bucket Sort
- Bingo Sort Algorithm
- ShellSort
- TimSort
- Comb Sort
- Pigeonhole Sort
- Cycle Sort
- Cocktail Sort
- Strand Sort
- Bitonic Sort
- Pancake sorting
- BogoSort or Permutation Sort
- Gnome Sort
- Sleep Sort – The King of Laziness
- Structure Sorting in C++
- Stooge Sort
- Tag Sort (To get both sorted and original)
- Tree Sort
- Odd-Even Sort / Brick Sort
- 3-way Merge Sort