Finding Minimum And Maximum (Application Of Divide And Conquer)

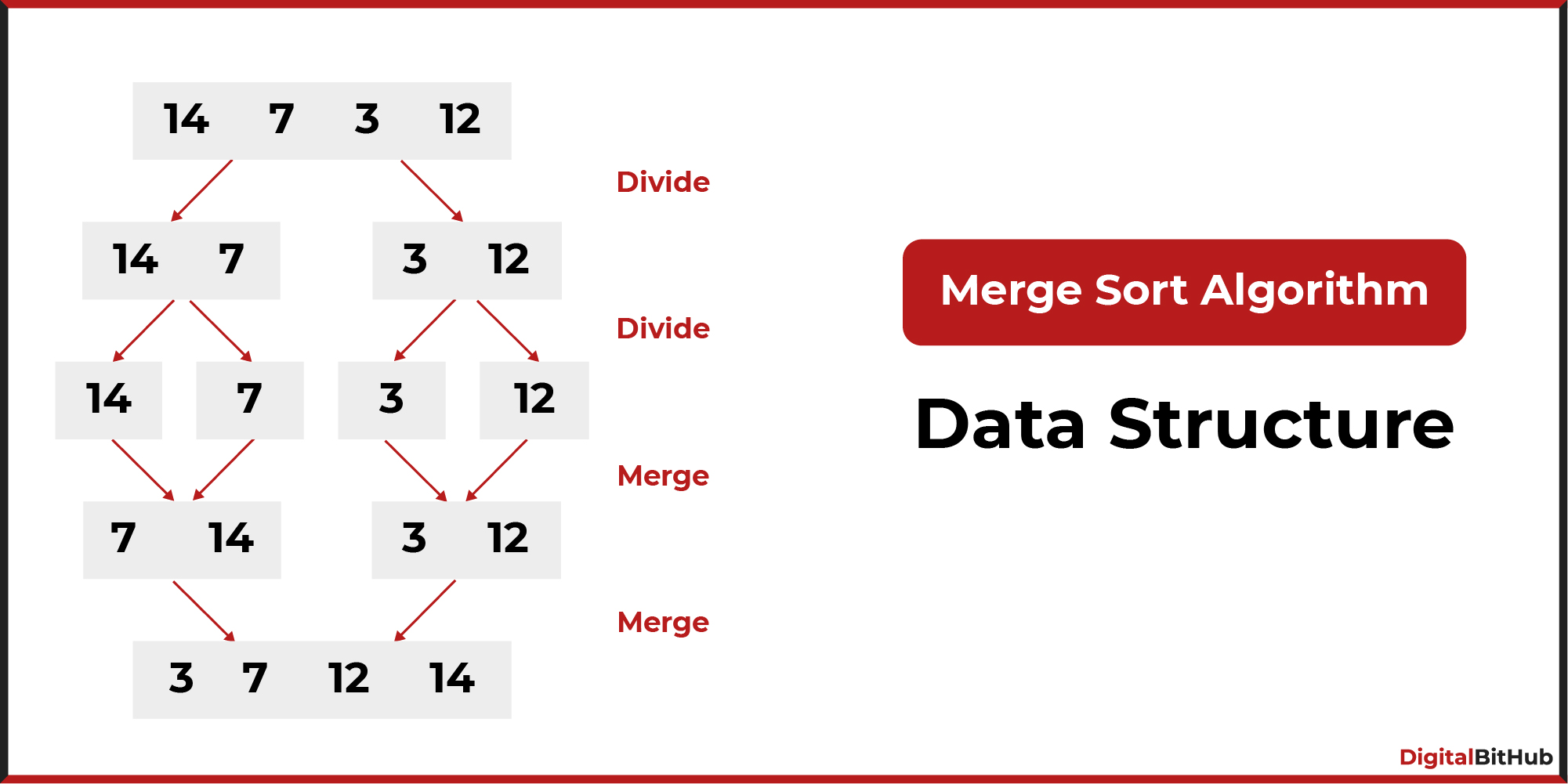
Finding a maximum and minimum element from a given array is the application of the Divide and Conquer algorithm.

There are various ways to this problem, but the most traditional approach to to solve this problem is the linear approach. In the linear approach, we traverse all elements once and find the minimum and maximum element.

In this approach, the time complexity to solve this problem is θ(n). 

Let's see the algorithm for the linear approach,
suppose A is the array of integers and n is the number of elements in the array A.

MinMax(A, n){
    int min = A[0];
    int max = A[0];
    for(int i = 1; i < n; i++){
        if(max < A[i])
            max = A[i];
        else if(min > A[i])
            min = A[i];
    }
    return (min, max);
}

Time Complexity for the above algorithm is T(n) = 2(n-1) + C ≈  θ(n).

Using Divide And Conquer Approach:

As we know in the divide and conquer approach, we first divide the problem into small problems and combine the results of these small problems to solve the main problem.

In Divide and Conquer approach:

• Step 1: Find the mid of the array.
• Step 2: Find the maximum and minimum of the left subarray recursively.
• Step 3: Find the maximum and minimum of the right subarray recursively.
• Step 4: Compare the result of step 3 and step 4
• Step 5: Return the minimum and maximum.

Let's see the algorithm for the Divide and Conquer approach, 

suppose A is the array of integers and n is the number of elements in the array A.

• i = 0 (Index of first element of array)
• j = n -1 (index of last element of array)

MinMaxDAC(A, i, j) {
    if(i == j)
        return (A[i], A[i]);
    if((j - i) == 1)
        if (A[i] < A[j])
            return (A[i], A[j]) 
        else 
            return (A[j], A[i]) 
    else {
        int mid = (i + j) / 2; 
        LMin, LMax = MinMaxDAC(A, i, mid); 
        RMin, RMax = MinMaxDAC(A, mid + 1, j);
        if(LMax > RMax)
            max = LMax;
        else 
            max = RMax;
        if(LMin < RMin)
            min = LMin;
        else 
            min = RMin;
        return (min, max);

Time Complexity for the DAC algorithm:

T(n) = 1,  if n = 1 or n = 2 

T(n) = 2T(n/2) + C, if n > 2

After solving the above recurrence relation,

T(n) = $\frac{3n}{2}-2$ ≈ Ο(n)

Conclusion

From the above two solutions, we can conclude that the linear approach does  2(n-1) comparisons and the DAC approach does only $\frac{3n}{2}-2$ comparisons.