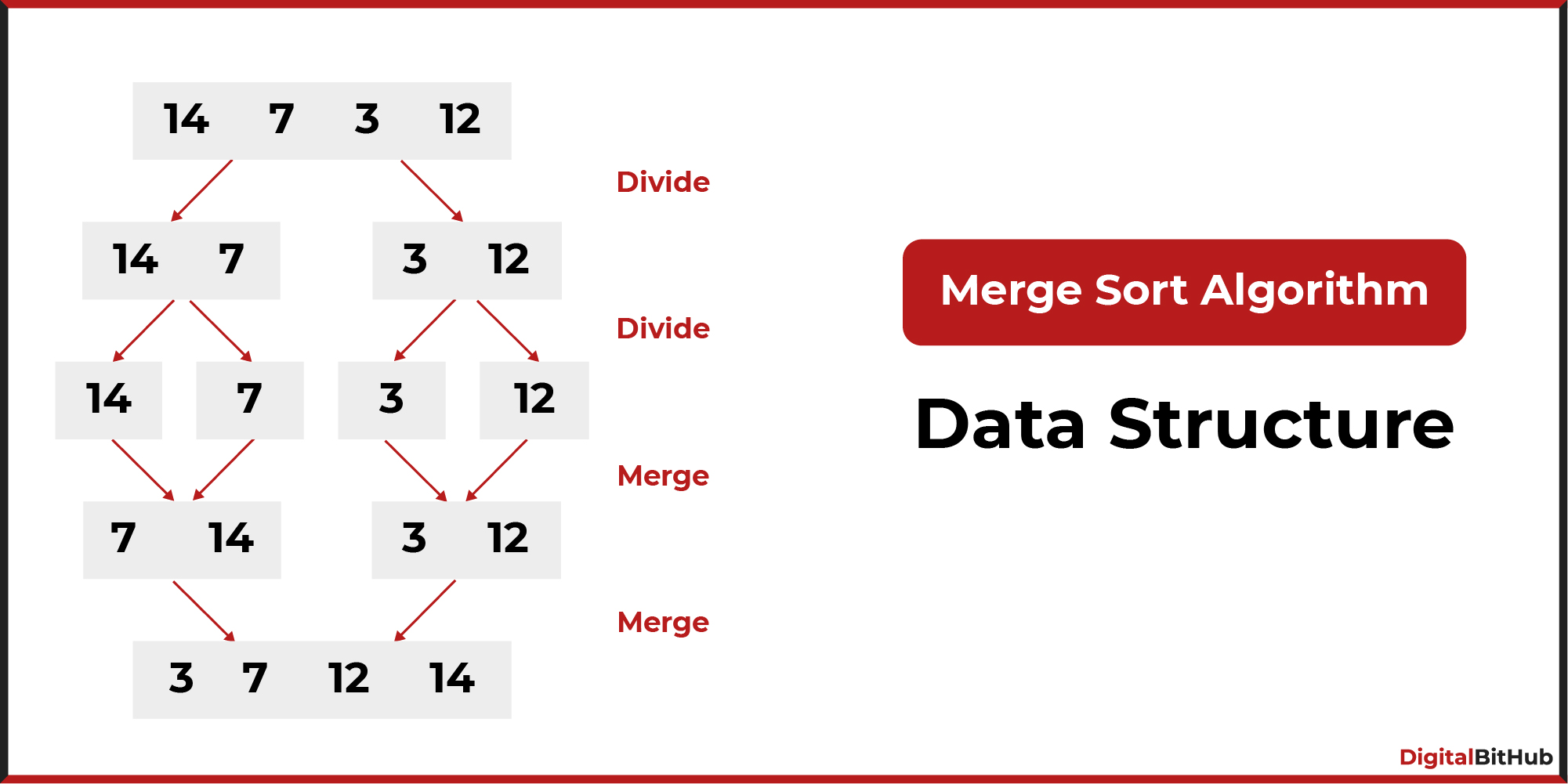
Algorithms

Let 𝐺 be any undirected graph with positive edge weights, and 𝑇 be a minimum spanning tree of 𝐺. For any two vertices, 𝑢 and 𝑣, let 𝑑1 (𝑢, 𝑣) and 𝑑2 (𝑢, 𝑣) be the shortest distances between 𝑢 and 𝑣 in 𝐺 and 𝑇, respectively. Which ONE of the options is CORRECT for all possible 𝐺, 𝑇, 𝑢 and 𝑣?

Consider the following recurrence relation:𝑇(𝑛) = 2𝑇(𝑛 1) + 𝑛2n for 𝑛 0, 𝑇(0) = 1.Which ONE of the following options is CORRECT?

Given an integer array of size N, we want to check if the array is sorted (in either ascending or descending order). An algorithm solves this problem by making a single pass through the array and comparing each element of the array only with its adjacent elements. The worst-case time complexity of this algorithm is

Consider the problem of reversing a singly linked list. To take an example, given the linked list below, the reversed linked list should look like Which one of the following statements is TRUE about the time complexity of algorithms that solve the above problem in O(1) space?

For parameters a and b, both of which are (1), T(n) = T(n1/a) + 1, and T(b) = 1. Then T(n) is

What is the worst-case time complexity of inserting n elements into an empty linked list, if the linked list needs to be maintained in sorted order?

Let G = (V, E) be a weighted undirected graph and let T be a Minimum Spanning Tree (MST) of G maintained using adjacency lists. Suppose a new weighed edge (u,v) VV is added to G. The worst-case time complexity of determining if T is still an MST of the resultant graph is

Let G = (V, E) be a directed, weighted graph with weight function w: ER. For some function f: VR, for each edge (u, v) E, define w'(u,v) as w(u,v)+f(u)-f(v). Which one of the options completes the following sentence so that it is TRUE?? "The shortest paths in G under w are shortest paths under w' too,_____".

Consider the array representation of a binary min-heap containing 1023 elements. The minimum number of comparisons required to find the maximum in the heap is ________?

Consider a graph G = (V, E), where V = {v1, v2,..., v100}, E = {(vi, vj) | 1 i j 100}, and weight of the edge (vi, vj)is |i-j|. The weight of minimum spanning tree of G is ______.