Unveiling the power of Dynamic Programming
In the broader landscape of algorithmic problem-solving, dynamic programming (DP) emerges as a powerful strategy, capable of efficiently addressing complex problems. Let's begin the journey of uncovering the fundamentals of dynamic programming, and exploring its fundamental concepts through real-world applications.
Essence of dynamic programming
Understanding Overlapping Subproblems
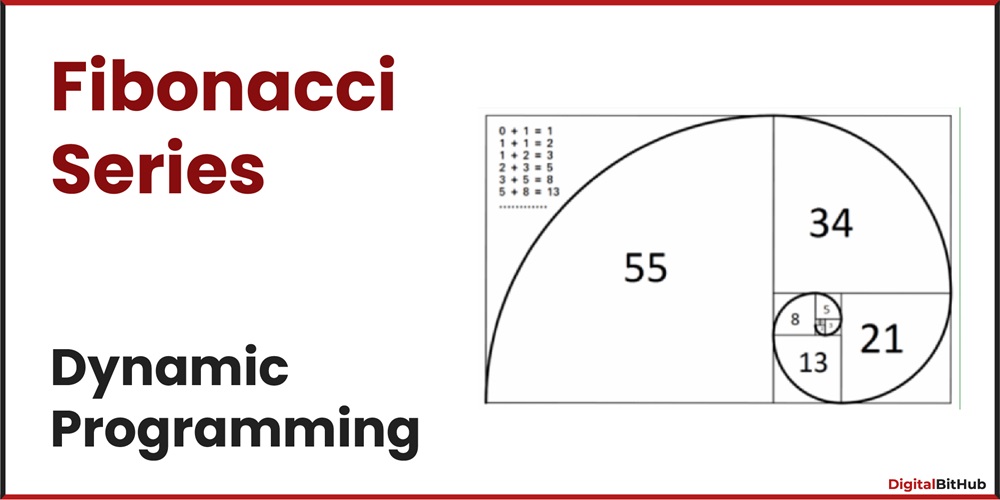
At the core of dynamic programming lies the concept of overlapping subproblems. It involves breaking down a complex problem into smaller, more manageable sub-problems. These sub-problems are often repeated, enabling us to store and reuse solutions rather than recalculating them unnecessarily. Consider a classic example of calculating Fibonacci numbers. Recursive approaches involve redundant calculations, while dynamic programming optimizes this process by storing previously calculated values, resulting in a more efficient solution.
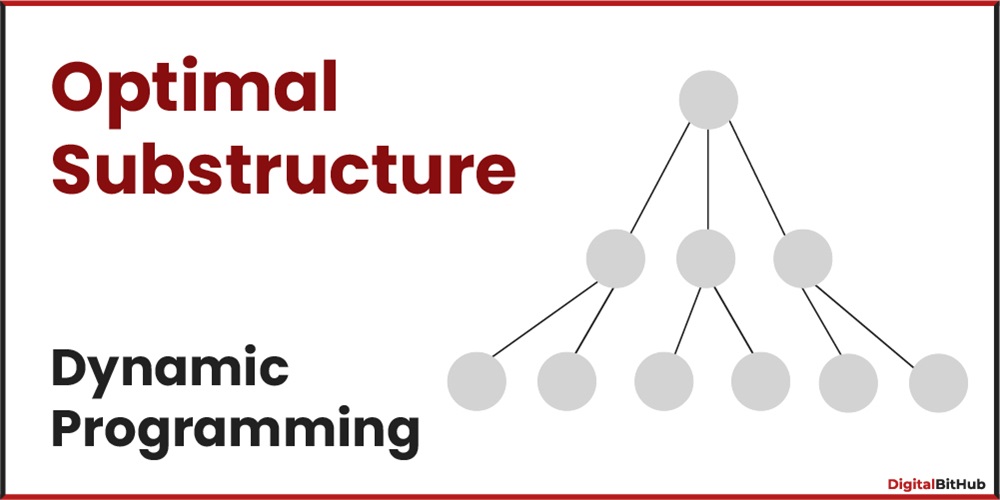
Adoption of optimal substructure
The second important concept is optimal subproblems, which state that an optimal solution to the overall problem can be created from optimal solutions to its subproblems. This property empowers us to generate solutions iteratively, ensuring that each step contributes to the overall optimal solution. Optimal substructure is a major reason behind the effectiveness of dynamic programming in solving a wide range of problems.
Contrasting dynamic programming with other techniques
In our exploration of dynamic programming, it is important to distinguish it from other problem-solving techniques such as divide-and-conquer, greedy algorithms, and brute force. Each method has its own strengths, but dynamic programming excels in scenarios where optimal solutions to sub-problems contribute significantly to the optimal solution to the broader problem.
Real-World Application of Dynamic Programming
1. Shortest path in a graph:
Imagine navigating through a network of interconnected points, aiming to find the shortest path between two locations. Dynamic programming efficiently solves this problem by breaking it into smaller sub-problems and optimizing the path-finding process. This application is ubiquitous in logistics, where minimizing travel distances is important.
2. Portfolio Management in Finance:
In finance, dynamic programming plays an important role in optimizing investment portfolios. By breaking down the complex task of portfolio management into smaller sub-problems, investors can make informed decisions, maximizing returns while managing risk. This application is fundamental in algorithmic trading and money management.
3. DNA Sequence Alignment in Biology:
In bioinformatics, dynamic programming is used for DNA sequence alignment. By breaking the comparison of biological sequences into smaller sub-problems, scientists can efficiently identify similarities and differences between genetic codes. It helps in understanding evolutionary relationships and genetic variations.
4. Resource Allocation in Project Management:
Project managers often face the challenge of optimal resource allocation. Dynamic programming provides a systematic approach by breaking the allocation problem into smaller sub-problems. This ensures that resources are used efficiently while meeting project deadlines and goals.
5. Network Routing in Telecommunications:
Telecommunications networks rely on efficient routing algorithms. Dynamic programming comes to the forefront in optimizing the routing process, reducing delays, and ensuring data travels through the network in the most efficient manner. This is important to maintain quality of service in telecommunication.
Wrapping Up the Prelude
This introduction not only provides a glimpse into the fascinating world of dynamic programming but also shows its real impact through real-world examples. As we delve deeper into this series, we'll highlight specific applications, algorithms, and optimization techniques that make dynamic programming an invaluable tool in solving myriad computational challenges.