An algorithm has to store several keys generated by an adversary in a hash table. The adversary is malicious who tries to maximize the number of collisions. Let k be the number of keys, m be the number of slots in the hash table, and k>m.
Which one of the following is the best hashing strategy to counteract the adversary?
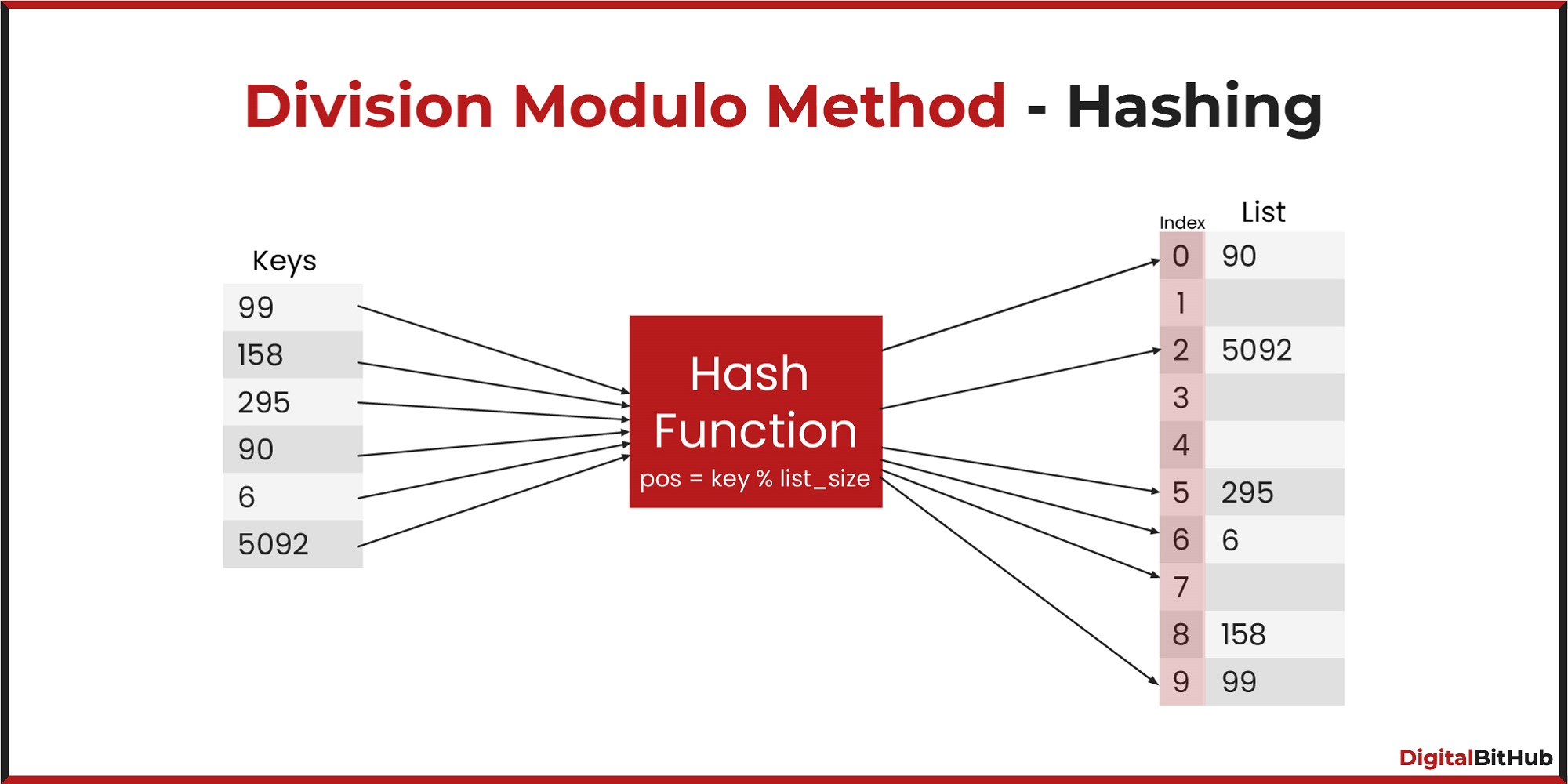
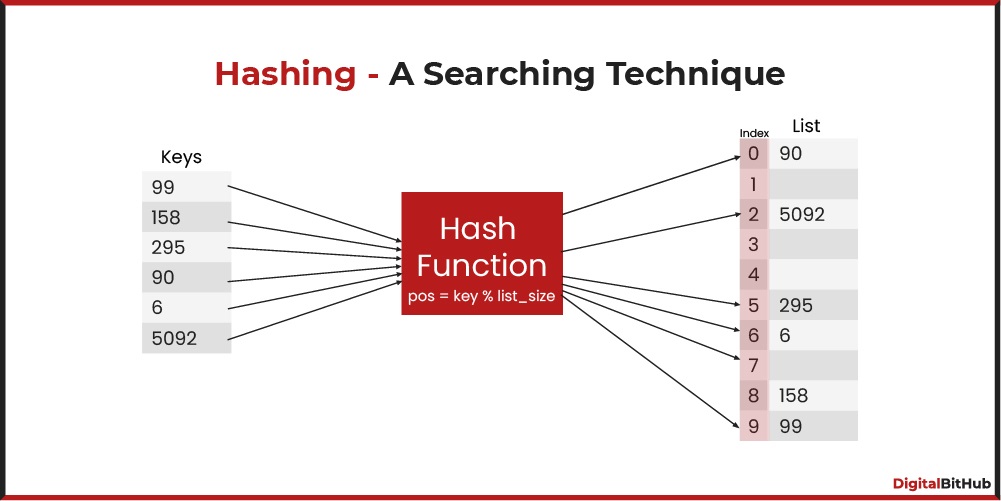
Division method, i.e., use the hash function h(k) = k mod m
Multiplication method, i.e., use the hash function
h(k) = ⌊m(kA − ⌊kA⌋)⌋, where A is a carefully chosen constant.
Universal hashing method.
If k is a prime number, use the Division method. Otherwise, use the Multiplication method.
Any fixed hash function is vulnerable to hash the key in the table because there is a chance that someone chooses the key in such a way that all the keys are hashed in the same slot, yielding an average retrieval time θ(n). This is the worst-case behaviour.
The only effective way to improve the situation is to choose the hash function randomly in such a way that is independent of the keys that are going to be stored. This approach is called Universal Hashing.
Know more about Division Modulo Hashing